Comment calculer le pgcd de deux nombres entiers naturels ?
C'est quoi le pgcd de deux nombres entiers ?
En maths, le PGCD (Plus Grand Commun Diviseur) de deux nombres entiers naturels donnés est le plus grand nombre entier naturel qui est en même temps un diviseur des deux nombres. C'est à dire lorsqu'on divise chacun des deux nombres entiers avec leur pgcd, on trouve un quotient entier positif et un reste nul.
Exemple: Le PGCD de 6 et 4 est 2.
Cela signifie que 2 est le plus grand nombre entier naturel qui est à la fois un diviseur de 6 et un diviseur de 4.
Comment trouver le pgcd de deux nombres entiers ?
Pour trouver le pgcd ou le ppcm de deux nombres entiers, il faut passer par deux étapes : la décomposition de chacun des deux nombres en produit de facteurs premiers et le choix des facteurs entre les deux produits de facteurs premiers des deux nombres.
Décomposition en produit de facteurs premiers
La décomposition en produit de facteurs premiers d'un nombre entier consiste à l'exprimer sous forme d'un produit ou tous les facteurs sont des nombres premiers. Les nombres premiers se trouvant dans le produit sont donc des diviseurs du nombre donné. Lorsqu'un facteur apparaît plusieurs fois dans le produit, on l'écrit sous forme de puissance.
Exemple : la décomposition en produit de facteurs premiers de 420 :
420 = 2^2 * 3 * 5 * 7
Pour trouver les facteurs premiers d'un nombre entier (qui n'est pas premier), on le divise successivement par les nombres premiers successifs (2; 3; 5; 7; 11;...) qui sont ses diviseurs. Car un nombre qui n'est pas premier est forcement un produit de nombres premiers.
Voici comment les facteurs premiers de 420 sont déterminés :
420/2 = 210
210/2 = 105
105/3 = 35
35/5 = 7
7/7 = 1 (la division s'arrête au quotient = 1).
Les facteurs premiers de 420 sont donc les diviseurs (nombres premiers) utilisés dans les divisions successives de 420 : 2; 2; 3; 5; 7
Choix des facteurs premiers
Lorsque la décomposition en produits de facteurs premiers des deux nombres entiers est effectuée, il reste à faire le choix des facteurs qui doivent entrer dans le calcul du pgcd ou du ppcm. On fait le choix des facteurs en tenant compte de trois critères :
1) facteurs communs ayant la même puissance ;
2) facteurs communs ayant des puissances différentes ;
3) facteurs non communs;
Un facteur est commun lorsqu'il apparaît dans les deux produits de facteurs premiers (des deux nombres), il n'est pas commun (non commun) lorsqu'il n'apparaît que dans un seul produit de facteurs premiers (de l'un des deux nombres).
Choix des facteurs dans le cas du pgcd
1) Si deux facteurs communs ont la même puissance on choisit l'un d'entre les deux;
2) Si deux facteurs communs ont des puissances différentes ont choisit le facteur ayant la puissance la moins élevée.
3) Les facteurs non communs ne sont pas choisis.
Exemple : Calculons le pgcd de 630 et 660
630 = 2 * 3^2 * 5 * 7
660 = 2^2 * 3 * 5 * 11
PGCD(630 ; 660) = 2 * 3 * 5
Alors PGCD(630 ; 660) = 30
Comment trouver le ppcm de deux nombres entiers ?
Choix des facteurs dans le cas du ppcm
1) Si deux facteurs communs ont la même puissance on choisit l'un d'entre les deux;
2) Si deux facteurs communs ont des puissances différentes ont choisit le facteur ayant la puissance la plus élevée.
3) Tous les facteurs non communs sont choisis.
Exemple : Calculons le ppcm de 630 et 660
630 = 2 * 3^2 * 5 * 7
660 = 2^2 * 3 * 5 * 11
PPCM(630 ; 660) = 2^2 * 3^2 * 5 * 7 * 11
Alors PPCM(630 ; 660) = 13 860
PGCD Java
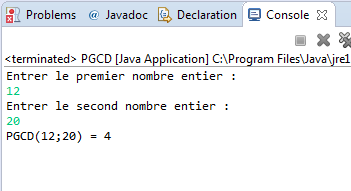
Le programme java ci-dessous, vous permettra de trouver le PGCD de n'importe quel couple de nombres entiers naturels que vous allez lui indiquer. Par exemple si vous donnez 12 et 20 le programme vous affichera :
PGCD(12;20) = 4
.
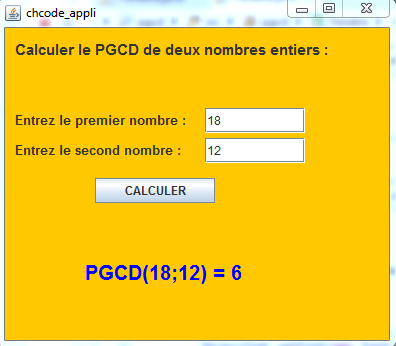
Le programme est fourni avec deux versions, une version exécutable dans la console java et une autre version à exécuter dans une fenêtre java.
La version du programme exécutable dans la console:
import java.util.Scanner;public class PGCD {
public static void main(String[] args) {
int diviseur=0;
Scanner sc = new Scanner(System.in);
System.out.println("Entrer le premier nombre entier :");
int n1 = sc.nextInt();
System.out.println("Entrer le second nombre entier :");
int n2 = sc.nextInt();
for(int i=1;i<=n1;i++){
if(n1%i==0&&n2%i==0){
diviseur=i;
}
}
System.out.println("PGCD("+n1+";"+n2+") = "+diviseur);
}
}
Exemple d'utilisation:
La version du programme munie d'une interface graphique:
Exemple d'utilisation:
Télécharger le code source
Un programme Java pour calculer le Plus Petit Commun Multiple (PPCM) de deux nombres entiers naturels
Le PPCM est une notion mathématique opposée au PGCD, quand on cherche à déterminer le plus grand nombre entier qui est un diviseur commun à deux nombres entiers dans le cas du PGCD, pour le PPCM, on cherche à trouver le plus petit nombre entier qui est un multiple commun de deux nombres entiers donnés. Par exemple le PPCM de 8 et 6 est 24.
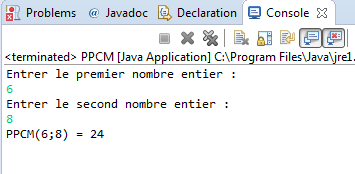
Le programme java ci-dessous, permet de calculer le PPCM de deux nombres entiers naturels donnés par l'utilisateur, par exemple, quand on donne: 10 et 4, ce programme java affichera: PPCM(10;4) = 20
La version du programme exécutable dans la console:
import java.util.Scanner;public class PPCM {
public static void main(String[] args) {
int multiple=0;
Scanner sc = new Scanner(System.in);
System.out.println("Entrer le premier nombre entier :");
int n1 = sc.nextInt();
System.out.println("Entrer le second nombre entier :");
int n2 = sc.nextInt();
for(int i=n1*n2;i>=n1;i--){
if(i%n1==0&&i%n2==0){
multiple=i;
}
}
System.out.println("PPCM("+n1+";"+n2+") = "+multiple);
}
}
Exemple d'utilisation:
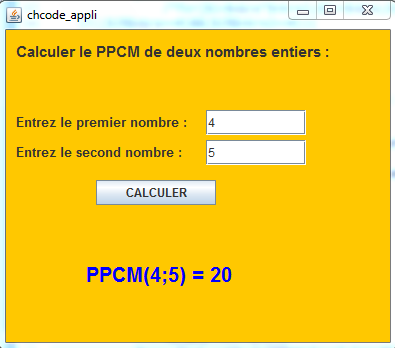
La version du programme munie d'une interface graphique:
Exemple d'utilisation:
Télécharger le code source
Un programme en (java eclipse) pour déterminer les multiples d'un nombre entier inférieurs à un autre nombre entier donné
Soit A et B deux nombres entiers naturels, si A est un multiple de B alors la division de A par B donnera un quotient entier et un reste nul. Par exemple 15 est un multiple de 3 parce que 15 divisé par 3 donne 5 comme quotient et 0 comme reste.
En mathématiques, un nombre entier naturel donné a un nombre infini de multiples, c'est pourquoi, le programme java ci-dessous va vous permettre de déterminer une liste des multiples d'un nombre entier donné qui sont inférieurs à un autre nombre entier que vous allez indiquer.
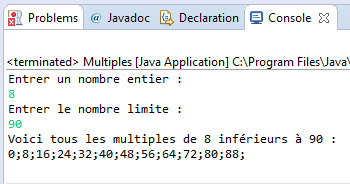
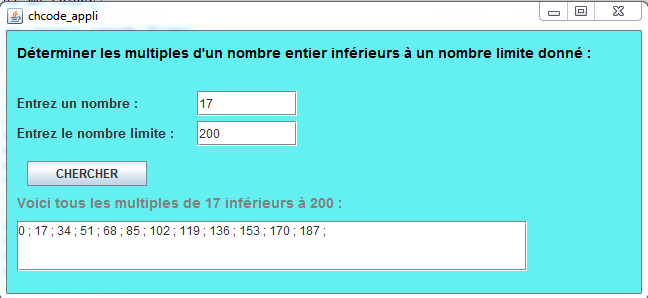
Si vous donnez successivement 6 et 20 par exemple, le programme comprendra que vous voulez afficher tous les multiples de 6 qui sont inférieurs à 20 et vous affichera : 0; 6; 12; 18
La version du programme exécutable dans la console:
import java.util.Scanner;public class Multiples {
public static void main(String[] args) {
int multiple=0;
String mess="";
Scanner sc = new Scanner(System.in);
System.out.println("Entrer un nombre entier :");
int nombre1 = sc.nextInt();
System.out.println("Entrer le nombre limite :");
int nombre2 = sc.nextInt();
if(nombre1>nombre2){
System.out.println("Erreur. Le nombre est
supérieur à la limite, augmentez la limite.");
}
else{
System.out.println("Voici tous les multiples
de "+nombre1+" inférieurs à "+nombre2+" :");
for(int i=0;nombre1*i< nombre2;i++){
multiple=nombre1*i;
mess=mess+multiple+";";
}
System.out.println(mess);
}
}
}
Exemple d'utilisation:
La version du programme munie d'une interface graphique:
Exemple d'utilisation:
Télécharger le code source